Algoritmo SA
Descripción del Algoritmo
El algoritmo de Simulated Annealing pertenece a la clase de
los algoritmos probabilísticos e iterativos. Pretende simular
el proceso de enfriamiento que se utiliza para los metales,
consistente en elevar la temperatura hasta que el material se
funde y, a continuación, disminuir la temperatura hasta que se
alcanza el punto de congelación.
F. Romeo y A. Sangiovanni-Vincentelli realizaron un análisis
teórico del algoritmo utilizando cadenas de Markov y demostraron
que, si se cumplen ciertas restricciones sobre el número de
iteraciones a cada temperatura, se genera, con probabilidad
igual a uno, un óptimo global. Desafortunadamente, este resultado
es asintótico, ya que puede ser necesario un tiempo de
computación infinito para garantizar la convergencia a la
solución óptima.
En los circuitos con un elevado número de componentes, la
optimización de las particiones es muy similar al proceso de
enfriamiento de un metal, que se describe a continuación.
- Calentamiento
- El material, en estado sólido, se calienta hasta que
alcanza un estado líquido amorfo. Cuanto más elevada
es la temperatura, más aleatorio es el estado.
- Enfriamiento
- Lentamente, se va disminuyendo la temperatura del metal.
Es preferible que el enfriamiento sea lento porque, de
este modo, el material puede alcanzar el equilibrio a
cada temperatura.
- Congelación
- Una vez que se ha alcanzado la temperatura de congelación,
los átomos del material están dispuestos de forma que
la energía global es mínima.
El algoritmo de Simulated Annealing trata de adaptar este
proceso a diferentes fases del diseño físico de un circuito
VLSI, y establece como objetivo la minimización de una
determinada función de coste, que, en el proceso de enfriamiento,
se corresponde con la energía asociada a cada estado del material.
A continuación, se exponen las diferentes fases que incluye
este algoritmo.
- Se disponen las celdas del circuito según una partición
inicial aleatoria y se toma una temperatura inicial
suficientemente elevada.
- Se eligen, al azar, dos elementos pertenecientes a
particiones distintas.
- Se calcula deltas,que representa la diferencia entre el
coste asociado al estado resultante del intercambio de
los elementos seleccionados en el paso 2, y el coste
asociado al estado previo.
Si deltas<0, se acepta el cambio, puesto que se ha
reducido el coste asociado al estado.
En caso contrario, se acepta el cambio con una
probabilidad que viene dada por una función
f(T), que puede adoptar diferentes formas,
entre ellas, la que se indica a continuación:
donde, T es la temperatura actual del sistema.
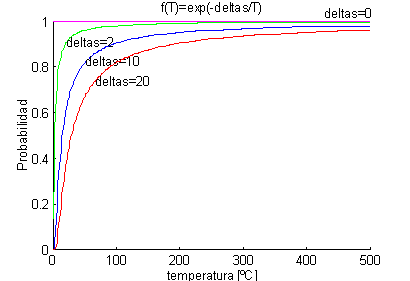
La figura siguiente muestra el comportamiento de esta
función con la temperatura, para distintos valores de
deltas.
La función f(T) elegida determina la capacidad del algoritmo
para escapar de los mínimos locales, en búsqueda de mínimos
globales.
Las características de esta función son:
- Los intercambios que implican un mayor incremento del
coste, se aceptan con menor probabilidad que aquellos que
suponen un pequeño aumento del mismo.
- A temperaturas elevadas, i.e., en las primeras iteraciones
del algoritmo, hay una mayor probabilidad de aceptar cambios
que impliquen un empeoramiento de la función de coste.
- Se comprueba si se ha alcanzado el equilibrio.
- Si no hay equilibrio, se vuelve al paso 2
- Si hay equilibrio, se avanza hacia la fase 5
- Se reduce la temperatura de acuerdo con un determinado patrón
de enfriamiento. Es posible elegir diferentes patrones:
| Progresión geométrica |
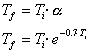 |
| Patrón exponencial |
Donde:
Ti, es la temperatura del sistema antes de aplicar el patrón de
enfriamiento.
Tf, es la temperatura del sistema después de aplicar el patrón
de enfriamiento.
El decrecimiento exponencial permite mejorar las prestaciones
del sistema, pero, como contrapartida, hace que el proceso
se ralentice mucho.
- Se comprueba si se ha alcanzado la temperatura de congelación.
- Si no se ha alcanzado, se vuelve al paso 2.
- Si se ha alcanzado, termina la ejecución del algoritmo.
Descripción de la implementación realizada
Este algoritmo, al igual que el algoritmo de Simulated Evolution y el algoritmo
de Kernighan-Lin, se ha implementado (en lenguaje C) dentro del programa partitio.exe.
Al ejecutar dicho programa (para una información detallada acerca de este particular, se recomienda consultar la información relativa al
al algoritmo de Kernighan-Lin), el usuario ha de elegir la opción Simulated Annealing y proporcionar un fichero de entrada que
contenga el número de bloques así como las interconexiones entre ellos.
Además del fichero de entrada, el programa solicita al usuario la introducción
de los valores de cuatro parámetros necesarios para la ejecución del algoritmo. Estos
parámetros son:
| Temperatura de fusión |
Este valor es la temperatura inicial del sistema. Cuanto
mayor es, más intensa es la búsqueda de una solución próxima
a la óptima. |
| Temperatura de congelación |
Cuando se alcanza esta temperatura, termina la ejecución del
algoritmo. Si se le da un valor pequeño, se emplea más tiempo
en la búsqueda de la solución. |
| Número de iteraciones en cada temperatura |
Este parámetro determina cuándo se considera que el sistema
ha alcanzado el equilibrio a una determinada temperatura.
Es decir, establece el número de intercambios que se realizan a cada temperatura y, una
vez alcanzado este valor, se reduce dicha temperatura. |
| Factor de decrecimiento de la temperatura |
Se ha implementado un patrón lineal de disminución de la temperatura.
Este factor determina el valor por el que se multiplica la temperatura
del sistema cada vez que éste alcanza el equilibrio. |
A partir de esta información, se distribuyen los bloques en dos
particiones, utilizando un método constructivo determinista; opcionalmente, es posible visualizar una representación gráfica de
esta distribución. El siguiente paso es la ejecución del algoritmo, tras lo cual,
también opcionalmente, es posible visualizar el reparto final de los
elementos. Por último, se genera el fichero de salida, en el
que se indica la distribución de los bloques obtenida.
Formato del fichero de entrada
Primera línea: Número de bloques del sistema (2N).
Líneas siguientes: Tiene que haber tantas líneas como bloques.
La correspondencia entre líneas y bloques es secuencial, i.e.,
la línea 2 corresponde al bloque 1, la línea 3 corresponde al bloque 2,... y
la línea (2N+1) corresponde al bloque 2N. En cada una de estas líneas,
se indica el número de interconexiones del bloque y los identificadores
de los bloques a él conectados; todo ello separado por comas.
Ejemplo de fichero de entrada
8
3,2,5,6
3,1,5,6
4,4,6,7,8
3,3,7,8
3,1,2,6
4,1,2,3,5
3,3,4,8
3,3,4,7
Formato del fichero de salida
El fichero de salida tiene cinco líneas. En la primera, se indica
a qué fichero de entrada corresponden los resultados. En las
líneas 2 y 4, se indican las particiones, y, en las líneas
3 y 5, se presentan, separados por espacios en blanco, los bloques
asignados a las particiones 1 y 2, respectivamente.
Ejemplo de fichero de salida
//Resultados de la partición del fichero bloques.txt.
PARTICIÓN 1:
3 4 7 8
PARTICIÓN 2:
1 2 5 6
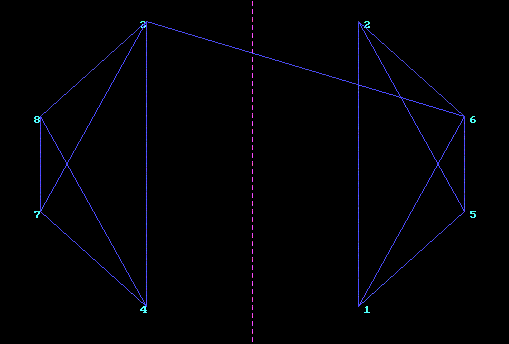
A continuación, se muestra la representación de las distribuciones
inicial y final de los bloques, correspondientes a dos ejecuciones del algoritmo SA
con distintos valores para los cuatro parámetros que rigen su funcionamiento, y
considerando el fichero de entrada anteriormente presentado.
La partición final 1 se ha obtenido tomando una temperatura inicial de 5000 ºC, una temperatura final igual a 10ºC, un
factor de decrecimiento de la temperatura igual a 0.9 y 50 iteraciones en
cada una de las temperaturas (condición de equilibrio). Mientras que la partición final 2 se ha obtenido tomando una temperatura inicial igual a
100 ºC, una temperatura final de 10 ºC, un factor de decrecimiento igual a
0.8 y 5 iteraciones en cada una de las temperaturas. Resulta evidente que
los valores dados a los parámetros que rigen el esquema de enfriamiento en el
primer caso son mejores que en el segundo caso. Esto justifica el hecho de
que la partición final 1 consiga reducir el número de cortes a 1, mientras
que, en el segundo caso, sólo se consigue reducir a 6. En comparación con
estos resultados, el algoritmo de Kernighan-Lin
consigue, para el mismo caso de entrada, un número de cortes igual a 1. Además, al ser
determinista, siempre obtiene ese resultado.